Содержание

Глава 6. Детальное планирование

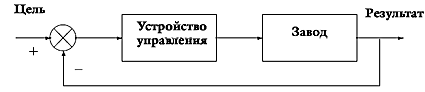
В главе 4 мы предложили идею планирования как разновидности обратной связи. Рис. 6.1 воспроизводит эту базовую идею. Теперь можно расширить нашу общую концепцию, чтобы рассмотреть конкретные свойства социалистического планирования, о которых мы уже писали.

Рис. 6.1. Механизм управления.

Как уже было показано, стратегическое планирование имеет дело с общей промышленной структурой экономики. В этой главе мы займемся детальным планированием, в процессе которого решается, сколько конкретных продуктов должно быть произведено, чтобы выполнить план, составленный в обобщенных показателях. Стратегический план может указывать, что на потребительскую электронику будет выделено 7 процентов национального дохода. Детальный план должен расписать, что это означает в терминах количества телевизоров каждой модели, количества каждого типа усилителей и т.д. А чтобы возможно было выполнить эти показатели, план должен определить также количество компонентов каждого типа, требующихся для сборки усилителей и телевизоров: 500000 цветных кинескопов с 14-дюймовой диагональю, 300000 – с 20-дюймовой диагональю, 12,5 миллионов керамических конденсаторов на 10 микрофарад, и так далее.

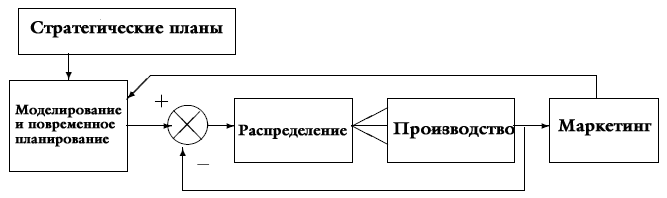
На рис. 6.2 показаны входные данные для процесса детального планирования. Моделирование и повременное планирование включают в себя построение детализированной модели работы экономики, чтобы можно было заранее предсказать, сколько сырья и деталей понадобится для производства запланированных товаров. Маркетинг – дающий для детального планирования косвенные данные – сообщает, оправдывает ли цена, которую люди готовы заплатить за товар, включение данного товара в план. Если люди не хотят платить столько же рабочего времени, сколько занимает производство данного товара, то его выпуск должен быть сокращен или прекращен вообще, а ресурсы переданы другому товару. Устройство предлагаемого нами маркетингового механизма обратной связи будет изложено отдельно в главе 8; а пока что мы ограничимся моделированием и распределением.

Рис. 6.2. Структура планирования.

Мы ввели в главе 3 таблицы входящих/исходящих потоков как средства расчетов общего содержание труда в товарах (input-output tables, в отечественной литературе они не совсем удачно называются таблицами затрат/результатов – прим. пер.). Этот метод представления экономики очень полезен и для формулировки и понимания проблемы детального планирования. Пример таблицы входов/выходов приведен в табл. 6.1. Читатель может также вновь заглянуть в пример, выписанный в табл. 3.2. Вспомните, что в таблице или матрице входов/выходов записываются потоки продуктов от каждой отрасли промышленности во все остальные. Каждая отрасль вносится два раза, занимая одну строку и один столбец. В нашем примере в строке, посвященной конкретной отрасли, указывается количество товаров, которые производит эта отрасль в качестве промежуточных продуктов, необходимых для других отраслей. Если первая строка относится к нефтяной промышленности, то числа в этой строке указывают количество нефти, поставленной в саму нефтепромышленность, в энергетику, в производство грузовиков и так далее. В колонке, соответствующей отрасли, можно увидеть количество всех продуктов, которые требуются как прямой входящий поток для этой отрасли. Например, если третья колонка представляет производство грузовиков, тогда, двигаясь снизу вверх, мы узнаем количество нефти, электричества и так далее, требующихся для сборки грузовиков.

Табл. 6.1. Часть таблицы входов/выходов

Для лучшего понимания полезно освоить некоторые базовые термины. Под валовым продуктом отрасли понимается общий поток, исходящий из нее, вне зависимости от его дальнейшего использования. Валовой продукт подразделяется на промежуточный продукт и конечный или чистый продукт. Промежуточный продукт – это часть произведенного отраслью продукта, предназначенная для использования внутри самой системы производства (например, уголь, использующийся в металлургии или сталь, использующаяся в производстве компьютеров). Конечный или чистый продукт – это остальная часть продукта, доступная для конечного использования (потребления – индивидуального или коллективного; чистых капиталовложений, предназначенных для развития производственной базы экономики).

Некоторые продукты по своей природе относятся в большей или меньшей мере к чисто промежуточным. Например, кроме немногочисленных любителей работы с металлом в качестве хобби, потребители просто не интересуются стальными листами, так что практически весь выход стальных листов будет являться промежуточным, участвующим в различных отраслях в производственном процессе. С другой стороны, некоторые товары являются чистыми конечными продуктами, не имеющими промежуточного применения (ни одна отрасль промышленности не использует пачки сигарет). Однако некоторые товары имеют и промежуточное, и конечное применение. Природный газ используют в домах для приготовления еды и отопления, а также в различных отраслях промышленности как исходный продукт для процесса проиводства.

Запомните еще один важный термин: технический коэффициент для любой упорядоченной пары отраслей показывает, сколько продукта одной из отраслей требуется (непосредственно) для производства единицы продукта другой отрасли. Если, например, для производства одного велосипеда требуется 10 килограммов стальных трубок, то технический коэффициент (стальные трубки, велосипеды) равен 10, если сталь измеряется в килограммах, или 0,01, если в тоннах. Обратите внимание, что полный непосредственный входящий поток стальных трубок для производства велосипедов можно найти, умножив общий выпуск велосипедов на соответствующий технический коэффициент. При коэффициенте 0,01 производство 2000 велосипедов потребует 2000 * 0,01 = 20 тонн стальных трубок.

Теперь мы готовы рассмотреть суть задачи, стоящей перед плановиками в социалистической экономике. Люди в конечном счете заинтересованы, чтобы экономика производила набор конкретных конечных товаров. Предположим, что у нас есть задание на производство этих товаров 1 . Его выполнение требует производства соответствующего количества промежуточных продуктов. Компьютеры в нужном количестве и нужного типа могут быть произведены, если от отраслей-поставщиков будет получено нужное количество пластика, стали, кремния и т.д., что, в свою очередь, требует, чтобы эти отрасли получили требующиеся им промежуточные продукты и так далее, в очень сложной сети взаимозависимостей.

Отсюда сама задача: как, начиная со списка желаемых конечных товаров, мы можем посчитать валовое количество продуктов каждого вида, требующихся для производства этих конечных товаров? (Те, кого математическая нотация приводит в уныние, могут пропустить несколько следующих абзацев и перейти сразу к выводу. Впрочем, мы используем самую несложные формулы). Рассмотрим простую маленькую систему всего с двумя отдельными отраслями. Обозначим через G валовой выпуск, через I – промежуточный выпуск и черех F – конечный выпуск. Нижние индексы, 1 и 2, обозначают отрасль. Поскольку валовой продукт равен промежуточному плюс конечному, мы можем описать нашу игрушечную экономику следующей парой уравнений, по одному на каждую отрасль:

G₁ = I₁₁ + I₁₂ + F₁

G₂ = I₂₁ + I₂₂ + F₂

В двойных индексах, стоящих возле промежуточных выходов (I) первое число означает источник продукта, а второе – его назначение. I₁₂, например, обозначает количество продукта первой отрасли, направляемое во вторую. На русском языке первое уравнение означает, что валовой выход первой отрасли есть сумма трех компонентов: промежуточного выпуска продукта номер 1, требующегося для самой первой отрасли (например, нефтяная промышленность потребляет некоторое количество нефти; для любой отрасли, не использующей свои собственные продукты, это число будет равно нулю); промежуточного выпуска продукта 1, требующегося для отрасли 2; и конечного или чистого выхода продукта номер 1.

Теперь прибегнем к небольшой хитрости: запишем каждый промежуточный выпуск (I) как произведение валового продукта (G) на соответствующий технический коэффициент. Вспомните описанные выше велосипеды и стальные трубки: промежуточное использование стальных трубок в велосипедной промышленности равно валовому выпуску велосипедов, умноженному на количество трубок, идущих на один велосипед. Если мы обозначим технические коэффициенты буквой a, получим следующую систему:

G₁ = a₁₁G₁ + a₁₂G₂ + F₁

G₂ = a₂₁G₁ + a₂₂G₂ + F₂

Теперь, даже не углубляясь в детали, мы видим, что задача имеет решение. После замены I на произведение a*G мы свели задачу к двум уравнениям с двумя неизвестными, а именно, валовым продуктам каждой отрасли. Простые, но утомительные алгебраические формулы должны дать нам соответствующий результат: уравнения, выражающие валовой продукт каждой отрасли в виде функции, зависящей только от конечных продуктов и технических коэффициентов. Когда мы нашли валовые продукты, потоки промежуточных продуктов, необходимые для каждой отрасли, легко рассчитать – так же, как мы делали это в примере с велосипедами 2 .

Математическая сторона задачи хорошо изучена после пионерских работ Василия Леонтьева и Джона фон Неймана 30-х и 40-х годов, а решение несложно найти, когда система не очень большая. Но если иметь дело с целой экономикой, единственный способ сделать систему «не очень большой» - выразить ее в сильно агрегированных терминах. Строки и колонки нашей таблицы могут, например, описывать «потребительскую электронику», «автомобили», «нефть и газ» и так далее. Для некоторых задач это приемлемо, но не годится для практического социалистического планирования. Если от плановиков требуются схемы, по которым можно управлять производством, в которых все экономические действия будут стыковаться друг с другом, то нужно с достаточной точностью указать входящие и исходящие потоки. Но в этом случае таблица потоков будет колоссальной, с миллионами строк и столбцов, а, следовательно, с миллиардами технических коэффициентов. Решение получившейся системы совместных уравнений – задача нетривиальная. Кроме того, еще до начала расчетов должно быть собрано огромное количество подробной информации (например, в форме технических коэффициентов).

Сбор информации и ее математическая обработка - одинаково важны обе эти задачи. Мы начнем рассмотрение с задачи расчета, предполагая, что необходимые данные уже «даны» (любимая фразочка экономистов); в главе 9 мы вернемся к проблеме получения данных.

Математические сложности, которые надо преодолеть, в сущности те же, что и при расчете трудовых стоимостей. Мы описывали их в главе 3. В принципе, задачу можно решить в лоб методом исключения Гаусса, но, как мы видели в главе 3, для очень больших систем это нереально. Как и при расчете трудовых стоимостей, надо использовать разреженную природу матрицы входов/выходов или «таблицы». Поскольку в подробной таблице будет огромное количество нулевых ячеек (показывающих, что зубная паста не используется в производстве сосисок, лес не нужен для производства очков и т.д.), будет лучше представить требования производства в форме связанных списков, а затем подыскать соответствующее итерационное решение.

Два основных итеративных метода (Якоби и Гаусса-Зайделя) могут использовать входные данные в форме связанных списков. Эти методы не дают непосредственного решения задачи, но могут выдавать последовательные, все более точные, приближения к нему. Для их применения в расчете входящих/исходящих потоков в экономике можно показать, что если существует единственное решение задачи (которое в принципе можно рассчитать напрямую), то они дают результаты, сходящиеся к этому решению (Varga, 1962).

Применение итеративного метода в данной задаче может быть продемонстрировано на простом примере. Необходимые для расчетов данные включают: 1) список требующихся конечных продуктов, 2) (ненулевые) технические коэффициенты и 3) некоторую первоначальную оценку валового выпуска каждого продукта. Эти исходные данные для валового выпуска вводятся в виде набора технических коэффициентов, затем рассчитывается количество каждого продукта, требующегося в качестве входа. На этой основе вычисляется новый набор показателей валового выпуска. Этот новый набор используется как входные данные для следующего цикла, и так далее. Если алгоритм сходится (то есть, задача вообще имеет единственное решение), то через некоторое время показатели валового выпуска будут все меньше изменяться от итерации к итерации. Алгоритм останавливается, когда приближенные значения показателей валового выпуска станут изменяться на величину, меньшую некоторой заранее заданной «малой».

Выбор начальных значений валового выпуска не критичен, поскольку сходимость алгоритма не зависит от начальных условий: если работают некоторые конкретные начальные условия, то будут работать и все остальные (опять-таки см. Varga, 1962). Однако, решение будет сходиться быстрее, если первоначальные оценки близки к правильным значениям. Плановики для выбора правильного порядка начальных значений могут, если это уместно, пользоваться прошлым опытом.

Временнóй порядок итеративного метода Якоби равен количеству выходных данных, умноженному на среднее количество различных непосредственных входных данных, требующихся для каждой итерации, умноженных на количество итераций, требующихся для получения удовлетворительного приближения. Если, допустим, имеется 10 миллионов продуктов и для каждого требуется 200 непосредственных входных данных, а всего нужно 100 итераций, то необходимо выполнить 2*10¹¹ инструкций. Компьютер со скоростью миллиард операций в секунду может закончить расчеты через 2*10³ секунд, то есть чуть больше, чем через полчаса.

Планирование в СССР

На этом месте возникают два вопроса о том, как соотносятся друг с другом описанные нами аргументы и опыт планирования в Советском Союзе. Во-первых, можно спросить: если расчеты, требующиеся для последовательного детального планирования так объемны и сложны, то как их ухитрялись проделывать в СССР до изобретения высокоскоростных компьютеров?

Остается только удивляться, как в СССР 30-х годов до изобретения компьютеров могли так успешно построить экономическую базу в виде тяжелой промышленности, используя методы централизованного планирования. Экономика в то время была, конечно, технологически намного проще, а планировалось относительно немного ключевых показателей. Но даже при этих условиях в годы первых пятилеток имелось немало случаев огромных расхождений между спросом и предложением. Огромный рост поставок материалов и предложения рабочей силы делал возможным достижение ключевых целей даже при дисбалансе расчетов.

Кроме того, надо заметить, что первые советские планы не рассчитывались методом, который предлагаем мы. Расчет обратным ходом – от целевого списка конечных продуктов до списка требующегося валового выпуска потоков, согласованный и подробный, была за пределами возможностей Госплана, государственного планирующего органа. Вместо этого плановики нередко отталкивались от показателей, уже выраженных в валовых терминах: столько-то тонн стали к 1930 году, столько-то тонн угля к 1935-му и так далее. Это первый опыт, вероятно, плохо повлиял на экономический механизм более позднего времени. Он положил начало «поклонению производству», когда производство гигантских объемов основных промежуточных продуктов стало рассматриваться как самоцель. С точки зрения входящих/исходящих потоков промежуточные продукты надо экономить всеми доступными методами. Целью должно быть производство минимальных количеств угля, стали, цемента и т.п., достаточных для изготовления желаемого объема конечных продуктов.

Второй возникающий вопрос является противоположностью первого: если математические и вычислительные методы, которые мы описали, хорошо известны, то почему советские плановики не стали работать намного лучше, когда в 80-х годах появились быстрые компьютеры?

Мы уже частично ответили на этот вопрос выше. Грубые по необходимости методы планирования 30-х годов отпечатались на развивавшейся позже системе. Из-за странного идеологического склероза последних сталинских лет – прерванного хрущевской оттепелью, но продолжившегося при Брежневе – к новым подходам в планировании обычно относились с подозрением. В литературе, посвященной советскому планированию, высказывается предположение, что сама идея начинать процесс планирования с конечных продуктов (которую мы защищаем) рассматривалась официальными хранителями ортодоксии как в некоторой степени «буржуазная».

Кроме того, интерес к новым, основанным на компьютерах, методам планирования в СССР вышел «из моды» как раз с появлением реальных технологических возможностей. Компьютерные системы, доступные советским плановикам в 60-е и 70-е годы (когда улучшение плановой системы было животрепещущей задачей), были примитивными по сегодняшним западным стандартам. Советские экономисты хорошо знали о потенциальных выгодах использования последовательного метода входящих/исходящих потоков, но оборудование, имевшееся в их распоряжении, позволяло проводить только анализ «маленьких», высокоагрегированных систем входов/выходов. Некоторые из них немного пригодились для упражнений в планировании связей между регионами (при исследовании взаимозависимости регионов СССР), но для повседневного детального планирования использовать их было нельзя. Анализ затрат/результатов по большей части остался академическим упражнением, а в целом внедрение компьютеров в советское планирование привело к разочарованию и краху первоначальных ожиданий 3 .

Важно заметить, что недоступность очень быстрых центральных компьютеров была не единственным и даже не самым важным ограничением. Как мы объясняли в главе 3, когда описывали расчет трудовых стоимостей, можно достичь тех же самых результатов, используя большую распределенную сеть намного более скромных персональных компьютеров, соединенных общегосударственной системой связи. Такое оборудование также было недоступно в те годы, когда советские экономисты всерьез задумывались об улучшении плановой системы. Дешевые ПК появились сравнительно недавно, а система связи в СССР была крайне отсталой (что знает любой, кто пытался позвонить из Москвы в Ленинград).

Кроме того, как мы увидим в главе 9, эффективное детальное планирование требует стандартизованной системы идентификации товаров, для чего, в свою очередь, нужны сложные компьютерные базы данных. В СССР плановики продолжали работать с системой так называемых «материальных балансов». Эта система, сводящаяся к составлению балансовых отчетов, показывающих отдельно для каждого товара источники производства и планируемое использование, была грубым приближением к методу входов/выходов. Плановики не могли эффективно рассчитать взаимодействие между такими балансами и, вдобавок, сама классификация товаров была неполной и непоследовательной.

В дело также вмешивалась политика. Наши предложения по планированию обязательно требуют свободного потока информации и всеобщего доступа к компьютерным системам, а в СССР времен Брежнева это было политически невозможно. Даже доступ к копировальному оборудованию строго контролировался из страха перед распространением диссидентских материалов.

И, в конце концов, компьютеризация, конечно же, не панацея. В механизме экономического планирования СССР имелось немало проблем, которые надо было решить, прежде чем добавление вычислительных мощностей могло принести ощутимые результаты (один пример: иррациональная и почти окаменевшая система цен, в которой цены на многие товары застряли на уровне, гарантировавшем дефицит и очереди).

Для эффективного детального планирования, похоже, требуются компьютерные и телекоммуникационные технологии, которые были доступны на Западе где-то с середины 80-х годов. Однако к этому времени идеологический климат в Советском Союзе сильно сдвинулся в сторону «реформ» рыночного направления. Похоже, что советские экономисты – по крайней мере, те, к кому прислушивались политические вожди при Горбачеве – не проявляли особого интереса к разработке тех видов алгоритмов и компьютерных систем, о которых мы пишем. Они, очевидно, потеряли веру в возможности эффективного планирования. Возможно, частично это была реакция на неудачи перехваленной компьютеризации, частично – отражение крена Запада в сторону рыночной экономики.

Детальное планирование и ограничения по ресурсам

Вернемся к главной линии наших аргументов. Мы показали, что сейчас планирующая организация реально может вести расчеты обратным ходом – от списка требующихся конечных товаров к списку валового выпуска, необходимого для сведения плана, даже если таблицы входов/выходов расписывают отношения между отраслями со всеми подробностями. Но расчеты, необходимые для построения детального плана, еще не завершены. Может быть, произвести товары в необходимых количествах окажется невозможным из-за «внешних» ограничений в количестве запасов средств производства и предложения труда.

Плановики могут рассчитать, что для выполнения плановых заданий требуется производство x терра-киловатт электроэнергии. Баланс системы входящих/исходящих потоков покажет, что имеется достаточное количество нефти, угля или урана для производства такого количества энергии, но хватит ли при этом мощности электростанций? Способность экономики к производству в определенный период ограничена доступностью запасов ресурсов длительного пользования, создание которых занимает много времени. Плюс количество доступного труда: достаточно ли трудовых ресурсов для выполнения плановых показателей валового выпуска?

Эти вопросы встанут немедленно после расчета конкретных показателей валового выпуска. Планирующая система может отправить в каждую отрасль промышленности рассчитанные требования валового выпуска, а компьютеры каждой отрасли (которые не должны быть супербыстрыми) могут затем рассчитать потребность в средствах производства и в труде, используя внутренние данные по каждой единице средств производства и трудовые коэффициенты. Затем потребности отраслей вводятся в центральные компьютеры, суммируются и сравниваются с центральными базами данных по запасам средств производства различных видов и с централизованными расчетами имеющихся трудовых ресурсов.

Если ограничения удовлетворены – то есть, отрасли запросили не больше каждого вида средств производства и не больше труда, чем имеется во всей экономике, - все хорошо и замечательно. Однако обратите внимание, что даже если удовлетворены общие ограничения, все же может возникнуть необходимость в перераспределении ресурсов между отраслями: центральная планирующая организация должна будет оптимизировать эти перестановки и выпустить соответствующие указания. Но если в этом месте обнаружится, что ограничения не удовлетворены, то потребуется некоторая коррекция плана. Первоначальные плановые цели конечного выпуска удовлетворены быть не могут (хотя «внешние» ограничения могут быть в какой-то мере ослаблены) и плановики должны начинать вычисления заново. Конечные продукты, имеющие наименьшую цену для общества, выкидываются из плана и расчет повторяется. Поскольку полный цикл расчетов будет занимать несколько часов, в худшем случае – дней, составления плана уложится в разумные сроки даже при нескольких повторениях.

Важность последнего пункта – то есть наличие ограничений производства, отличных от заложенных в систему входящих/исходящих потоков – на практике зависит от периода планирования. Если составляется план на сравнительно долгий период, то ограничения по ресурсам становятся менее важными. Если требуется бóльшее количество энергии, то можно построить электростанции. В пределе единственными «внешними» ограничениями системы входов/выходов экономики являются трудовые ресурсы и доступность невозобновляемых природных ресурсов. В этом случае приведение плановых показателей конечного выпуска в соответствие с внешними ограничениями должно быть относительно простым. И наоборот, чем короче период планирования, тем более важными становятся «внешние» ограничения по ресурсам. Любые средства производства, строительство которых требует больше времени, чем планируемый период, должны считаться ограничениями по ресурсам; если период планирования совсем короткий, то становится важным количество запасов материалов. Один из авторов разработал компьютерный алгоритм, удобный для сведения плана в такой ситуации. Этот алгоритм значительно отличается от стандартного подхода «затраты/результат», описанного выше. Теоретическая основа альтернативного алгоритма представлена в следующем разделе, вместе с реальным примером его применения.

Новый алгоритм сведения плана

Предположим, что мы начинаем с годового списка продуктов, необходимых для выпуска 100000 различных потребительских товаров. Показатели могут быть консервативными, и в этом случае часть ресурсов не будет использоваться, или, наоборот, избыточными, такими, что не могут быть достигнуты с имеющимися ресурсами. Мы хотели бы узнать, нужно ли уменьшить или увеличить плановые цели, чтобы ресурсы, в том числе существующие в экономике машины различных видов, использовались эффективно. Вряд ли для этого достаточно изменить на х процентов цифры выпуска для всех потребительских товаров. Выпуск одних товаров должен быть увеличен или уменьшен больше, чем других.

Если у нас ограниченное количество овец и простаивающие мощности в химической промышленности, нам надо знать, как это повлияет на количество произведенных шерстяных и акриловых свитеров. Надо ли сократить количество шерстяной одежды? Как это повлияет на производство акриловой? Сколько вязальных станков надо переключить с производства шерстяных вещей на акриловые?

Предположим, что для любой из тысяч линий по производству трикотажа мы можем выделить свободные вязальные машины. Все простаивающие мощности можно использовать на производстве конкретной модели свитера: ядовито-синего цвета с лиловой надписью «Спорт в Сен-Тропе» спереди, но сомнительно, что такое решение порадует потребителей. Нам требуется набор правил, по которым компьютеры смогут решить, какими должны быть осмысленные изменения плановых заданий в свете ограничений по ресурсам. Мы разработали компьютерную программу, которая выполняет такие изменения, основываясь на экономическом принципе уменьшающейся предельной полезности. Полное изложение алгоритма можно найти в Cockshott, 1990.

Функция гармонии

Алгоритм использует методы, разработанные для имитации нейросетей (раздел теории искусственного интеллекта). Исследователи в этой области предложили анализировать нейросистемы с помощью концепций термодинамики. Нейросистема состоит из большого количества сущностей, нежестко связанных друг с другом, и поэтому попадает в абстрактную категорию задач, изучаемых статистической механикой. Уже известно, что термодинамические концепции – энергия, энтропия и релаксация - могут быть с пользой применены к нейронным моделям. Каждый нейрон, подобно атому в твердом теле, связан с каким-то подмножеством всей совокупности, и взаимодействует с ним. В обоих случаях у нас имеются большие совокупности, в которых выполняются стохастические законы 4 , на которые влияют локальные взаимодействия. Можно определить соответствующий эквивалент энергии для нейронной сети – в общих чертах, это величина, показывающая, насколько близко поведение сети соответствует желаемому. Доказано, что если ввести в поведение нейросети вычислительный аналог температуры, то с помощью процесса релаксации можно заставить сеть стабилизироваться в районе желаемого поведения.

И снова, пользуясь аналогией, можно сказать, что нейронные сети и кристаллы на некотором уровне абстракции подобны экономике. В экономике отрасли связаны друг с другом локальными взаимодействиями. В этом случае мы имеем дело с отношениями поставщик-пользователь, а не с синаптическими соединениями или электростатическими силами, но абстрактное сходство имеется.

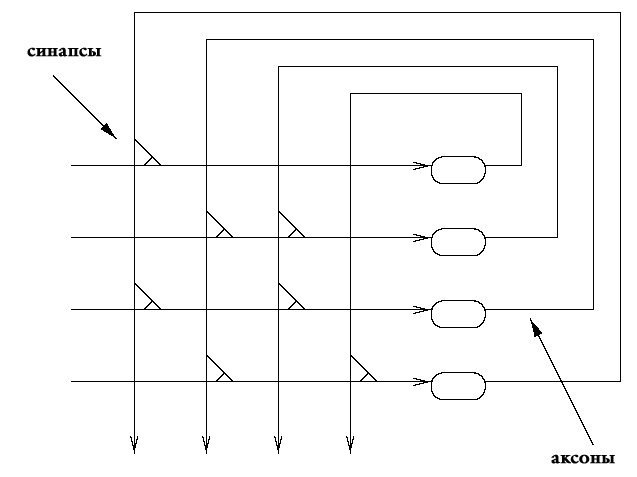
Обратите внимание на сходство между нейронной сетью на рис. 6.3. и матрицей входов/выходов. Колонки на диаграмме представляют выходы нервных клеток, изображенных справа. Синапсы посылают входную информацию клеткам, представленным строками. По строкам суммируется уровень полученного возбуждения. Уровень возбуждения на входах в свою очередь определяет уровень выхода на аксонах. Мы можем провести аналогию с колонками таблицы входов/выходов, которая изображает уровень действий отрасли. Назовем синапсы S_ij, где i – номер строки и j – номер колонки. Сила соединения на S_ij показывает количество продукта i-той отрасли, использованного для производства одной единицы продукта j-ой отрасли. Теория нейросетей предсказывает, что такая сеть достигнет распределения возбуждения, отражающего веса синапсов. Получившиеся уровни возбуждения на клетках будут представлять собой относительные интенсивности, с которым должны работать соответствующие отрасли. Нейронные сети можно математически моделировать. Отсюда следует, что мы можем сбалансировать экономику теми же математическими методами релаксации, которые используются при моделировании нейросетей. Нам только нужно найти аналог энергии, который можно минимизировать.

Рис. 6.3. Стилизованная нейросеть.

Работающие с нейронными сетями часто ставят задачу наоборот – вместо минимизации энергии они максимизируют нечто под названием «гармония». Формально, это величина, обратная энергии, но интуитивно она понятнее. Нейросеть установлена в состояние максимальной гармонии, когда она обучена и дает «правильные» ответы на внешние стимулы.

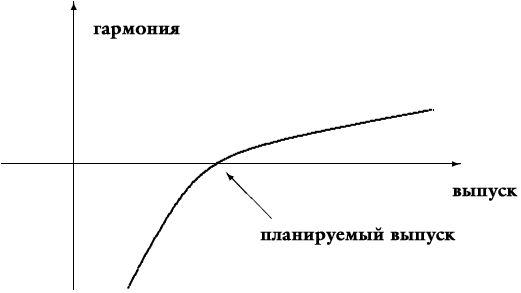
Мы можем применить понятие гармонии и к экономике. Мы определяем функцию гармонии для каждой отрасли в форме, показанной на рис. 6.4.

Рис. 6.4. Функция гармонии.

Как видите, гармония резко становится отрицательной, если чистый выпуск продукта (выпуск за вычетом потребления продукта другими отраслями) падает ниже целевого показателя. Гармония плавно становится положительной, если мы превышаем целевой показатель. Это означает, что проблемы, вызванные нехваткой продукта, более серьезны, чем выгоды, получаемые от его избытка. Иллюстративная функция с такими свойствами показана ниже в алгоритмической форме:

Пусть u = (выпуск – цель) / цель. Если u < 0, то гармония = -u², иначе гармония = √u.

Идея состоит в том, что люди от каждой потребляемой дополнительной единицы конкретного товара получают все меньшее удовлетворение. Первый раз, когда родственники дарят вам на рождество чайник, вы искренни им благодарны; на пятый раз благодарность будет уже несколько натянутой. Отсюда следует, что дополнительное общественное удовлетворение от превышения целевых показателей выпуска обычно довольно резко обрывается, и люди будут больше раздражаться на нехватку, чем радоваться изобилию. Мы можем моделировать это состояние показанной выше функцией гармонии.

Если выпуск товара находится на целевом уровне, мы считаем гармонию для этого товара равной нулю. Если выпуск превышает целевые показатели, гармония положительна, а если не достигает их – то отрицательная. Эта функция гармонии используется компьютером как руководство для корректировки показателей выпуска. Наша цель – максимизировать гармонию для всей экономики, чтобы привести ее в состояние баланса.

Шаги алгоритма

1) Случайным образом распределяются ресурсы по отраслям. Распределение сделано случайным намеренно, но происходит оно только в компьютере, продукты в реальной экономике при этом никуда не движутся. Мы используем случайное распределение, потому что, если наш метод релаксации работает, то все равно, с какого состояния начинать.

2) Для каждой отрасли определяется, какие ресурсы, доступные в настоящее время, служат ограничивающим фактором, то есть являются узким местом производства.

3) Каждая отрасль отказывается от некритичных ресурсов (то есть избыточных сверх требующихся, с учетом ограничивающих факторов), и они передаются в общий резерв. При этом производство не может уменьшиться по определению, а следовательно, не изменится и гармония. Обратите внимание, что перераспределение происходит только в памяти компьютера; в реальном мире ничего перераспределяться не будет, пока алгоритм не завершит работу.

4) Рассчитывается гармония для каждой отрасли.

5) Рассчитывается средняя гармония для всей экономики.

6) Отрасли сортируются в порядке возрастания гармонии.

7) Начиная с отраслей с самой большой гармонией, сокращается объем их выпуска, пока уровень производства не станет таким, что соответствующая ему гармония сравняется со средней по экономике. Это легко проделать, поскольку функция гармонии обратимая (то есть, мы можем рассчитать по уровню гармонии соответствующий уровень производства). Освобожденные таким образом ресурсы передаются в общий резерв.

8) Начиная с отраслей с наименьшей гармонией, им выделяются ресурсы из общего резерва, а их производство увеличивается до уровня, соответствующего средней гармонии.

9) Рассчитывается новая средняя гармония. Если она значительно отличается от старой, возвращаемся на шаг 6.

Этот алгоритм в конце концов уравнивает гармонию для всех отраслей. После всего лишь десятка итераций средняя гармония будет изменяться не более, чем на 1 процент. Однако у него есть недостаток: он выводит экономику только на локальный максимум гармонии. Если поэкспериментировать с представленным алгоритмом на компьютере, обнаружится, что в экономике остаются неиспользованные ресурсы, а общий уровень производства получается ниже, чем мог бы быть. Интуитивно мы можем понять, что это – результат очень сильной склонности алгоритма оставаться в области средней гармонии, с которой начались расчеты.

Можно преодолеть этот недостаток, если ввести отклонение в сторону увеличения производства. На шаге 7 вместо уменьшения производства отраслей с высокой гармонией мы корректируем их выпуск, пока гармония не станет равной (средняя + B), где B – отклонение. При запуске программы мы устанавливаем большое значение B, а на каждой итерации его уменьшаем. В результате сначала уменьшится выпуск только для отраслей с очень высокой исходной гармонией, а отрасли с низкой гармонией продолжат выпуск без изменений. Как следствие, средняя гармония будет расти на каждой итерации и система в конце концов стабилизируется возле максимальной средней гармонии.

Если правильно выбраны структуры данных, то время работы алгоритма примерно линейно зависит от объема данных. Другими словами, задача со 100 отраслями потребует в 10 раз больше времени, чем задача с 10 отраслями. Как и для традиционного анализа затрат/результатов, описанного выше, важно представлять таблицу входов/выходов не массивом, а воспользоваться тем, что – это очень разреженная матрица и представлять ее с помощью связанных списков. Временнóй порядок алгоритма тогда будет равен примерно nm, где n – количество отраслей, а m – среднее число входов для отрасли. Алгоритм достаточно прост, тестовый расчет плана с примерно 4 тысячами отраслей занял на рабочей станции «Сан» около 300 секунд. «Сан» выполняет примерно 3 миллиона операций в секунду. Поскольку затраты времени возрастают линейно, сведение плана для экономики с 10 миллионами продуктов займет на популярном микропроцессоре 68020 примерно миллион секунд (меньше двух недель). Потребуется также около тысячи мегабайт места. Это не фантастическая цифра: всего лишь эквивалент тысячи ПК, который будет стоить около полумиллиона фунтов при нынешних ценах.

Британская компания «Мейко» разработала мультипроцессор, который использует для скоростных расчетов до 1024 микропроцессоров одновременно. Предполагается, что эта машина будет использоваться для моделирования физики частиц. Она способна выполнять 10000000000 операций в секунду. Если мы запустим задачу на «Мейко» с 1024 процессорами, на каждом из которых стоит 4 мегабайта памяти, план для большой экономики будет рассчитан за 10 минут. (Процессор «Моторолла 68020» имел тактовую частоту примерно в 15 Мгц, современные (2006 г.) процессоры – 1,5 Ггц. Винчестер на 120 Гигабайт стоит сейчас около 60 долларов. Отсюда следует, что предлагаемые авторами расчеты теперь без всякого «Мейко» можно выполнить на стандартном ПК у себя дома - прим. пер.).

Кроме расчета пригодного для использования набора показателей выпуска, алгоритм также выполняет и побочную работу – правильно распределяет ресурсы и сырье между отраслями. Эта как раз та детальная информация, которая требуется от плана.

Мы доказали, что существуют методы расчетов, позволяющие проводить детальное планирование экономики в терминах физических единиц без использования денег или цен. Методы удобны для вычисления и могуть быть реализованы на высокопроизводительных компьютерах, которые уже сейчас используются, например, в физике частиц и прогнозировании погоды. Их можно рассматривать как предварительное моделирование процесса достижения равновесия, к которому предположительно стремится идеальный рынок.

Экономическая кибернетика в Чили

Один из наиболее интересных экспериментов с компьютеризированным планированием и управлением экономикой был проведен в Чили при правительстве Альенде с 1972 по 1973 год. Система была разработана Стаффордом Биром и описана в его книге «Мозг фирмы» 5 . Целью Бира было обеспечить децентрализованное управление экономикой в реальном времени. Поскольку его система представляет собой практический пример регуляторных механизмов общего типа, которые предлагаем мы, будет полезным кратко описать ее характеристики.

При использование обычных статистических методов, доступных западным правительствам, экономическая статистика нередко попадает на столы лиц, принимающих решения, устаревшей на много месяцев. В результате принимаемые решения могут пытаться разрешить кризис, который уже произошел несколько месяцев назад. Поскольку политические инструменты, доступные правительству, также действуют медленно, могут быть приняты решения, эффект от которых окажется противоположным задуманному. После краха фондовой биржи 1987 года британское правительство испугалось рецессии и в 1988 году уменьшило налоги. Ко времени, когда это постановление стало действовать, спрос уже и так рос, поэтому результатом стало нарастание инфляции в 1989 году. Задержки при доступе к данным означают, что будут предприняты совершенно неадекватные действия (хотя в данном случае к сокращению налогов вела и сильная идеологическая тяга, не зависящая от макроэкономических причин).

Таких извращенных эффектов, когда обратная связь вызывает в системе еще худшие биения, можно избежать, если управляющие располагают свежей информацией и у них есть средства немедленно предпринять соответствующие действия. Компьютерная сеть в Чили, позволяющая этого добиться, была готова всего через четыре месяца, к большому удивлению скептиков, считавших, что для создания сети понадобятся годы. Задача была решена с помощью компьютерных технологий начала 70-х годов и очень ограниченных возможностей связи, которыми располагала бедная страна вроде Чили. Микроволновые и телексные каналы соединили все главные промышленные центры с компьютерами в столице. В этих рамках оказалось возможным предоставлять правительству экономическую информацию с задержкой не более, чем в один день. Более современное оборудование позволило бы улучшить этот результат.

Информация представлялась в графической форме. Большие экраны в «Центре управления» выводили аннотированные потоковые графы, показывающие взаимодействия между частями экономики. На графических дисплеях не использовали цифровые показатели. Размер потоков между различными секторами изображался шириной линий, их связывающих. Отрасли и сектора отображались как прямоугольники со столбчатыми диаграммами внутри, указывающими, какая часть мощности отрасли сейчас используется. В комнате стояли сиденья для семи человек – это самое большое число людей, которое может с пользой участвовать в обсуждении. Большие кнопки на подлокотниках стульев использовались для управления дисплеями и подсветки определенных показателей.

Идея Центра управления была позаимствована из военного опыта воздушной обороны. Как и на войне, информация в реальном времени выводилась для принятия немедленных решений. Решения можно было проверить с помощью компьютерного моделирования, которое показывало, каковы будут последствия конкретных действий. При необходимости комната использовалась также как штаб-квартира – когда шла борьба с бойкотом правительства, введенным частными компаниями-грузоперевозчиками. Компьютерная сеть позволила правительству мобилизовать все доступные транспортные ресурсы для обеспечения перевозки товаров.

Задумывалось, что Центр управления будет установлен в каждой отрасли промышленности и даже на каждом заводе. Сложные статистические программы анализировали потоки данных, получаемых от нижних уровней системы, и находили любые существенные изменения. Люди, принимающие решения, защищались от информационной перегрузки, им выводились только важные данные, по которым нужно было принять решения. Заводской Центр управления выдавал бы предупреждения, если бы нормальный ход работы оказался нарушенным. Если компьютеры обнаруживали сбой, они предупреждали Центр управления и включали часы. Если Центр за определенное время не решил проблему, посылался сигнал тревоги в следующий Центр, расположенный выше в иерархии. Это давало возможность каждому подразделению действовать в рамках своей компетенции, не ставя под опасность работу всего социального организма. Планировалось, что в Центре управления на уровне фабрики будут работать представители местных рабочих комитетов. За этим решением стояло демократическое убеждение, что современные визуальные и компьютерные средства позволят людям управлять заводом без долгих тренировок.

Кровавый переворот, приведший к власти Пиночета и проложивший дорогу фридмановским монетаристским экспериментам с чилийской экономикой, смел все. Центры управления погибли вместе с Альенде и демократией в обгоревших руинах президентского дворца.

Примечания

1  Откуда взялись эти задания – вопрос отдельный. Мы уже кратко касались его в главе 5 и подробнее рассмотрим в главах 8 и 13.

2  Если уравнений много, удобнее представить их в форме матрицы. Тогда уравнения, приведенные в тексте, будут выглядеть следующим образом:g = Ag + f,где g обозначает вектор (n x 1) валовых продуктов, f – вектор (n x 1) конечных продуктов, а A – матрицу (n x n) технических коэффициентов (n – число отраслей в системе). Такая система может быть решена следующим образом: g = Ag + f → (I-A)g = f → g = (I-A)^–1f. (Здесь I – единичная матрица n x n). Другими словами, получается, что мы можем найти ответ - список требующихся валовых входов, инвертировав матрицу Леонтьева (I-A) и умножив ее на вектор конечных продуктов f.

3  Для оценки советского опыта использования компьютеров в планировании 70-х годов см. Martin Cave (1980), наши взгляды по этому вопросу более подробно изложены в Cottrell and Cockshott (1993b).

4  Стохастические законы означают, что объекта подчинен законам случая, которые невозможно предвидеть точно. Возможно лишь определить усредненное поведение объекта.

5  См. также «Afterword to Beer», 1975.