Глава 6. Вероятностный подход к закону стоимости

В этой главе мы применим вероятностный подход к фундаментальному вопросу политической экономии: существует ли отношение и если да, то какое, между временем, требующимся людям для производства вещей, и ценами, по которым они эти вещи обменивают?

6.1. Вероятностные модели

Если мы знаем возможные исходы определенной ситуации, естественно спросить, насколько они вероятны. Вероятность события — это число в интервале [0, 1], где 0 представляет невозможное событие и 1 — то, которое обязательно произойдет.

Например, если мы много раз будем подбрасывать монету, то вскоре обнаружим, что примерно в половине случаев выпадают орлы, а в половине — решки. Поэтому, хоть мы и не можем предвидеть исход конкретного броска, мы можем сказать, что орел или решка одинаково вероятны или, точнее, вероятность орла или решки — одна вторая, P(X=орлы) = P(X=решки) = 1/2, где X — исход подбрасывания монеты.

Знание P(X=орлы)=1/2 означает, что примерно в половине случаев монета упадет орлом. Собственно, это вероятностное предсказание частоты определенного исхода. Оно говорит не о том, что произойдет в действительности, а лишь о том, что вероятно произойдет, учитывая наше знание о возможных исходах. Хотя и более слабое, чем детерминированное предсказание, предсказание вероятностное тоже очень полезно для практических действий. Например, знание того факта, что определенный район имеет высокую вероятность землетрясений, указывает нам строить прочные дома, даже если мы не знаем точно, когда именно начнется землетрясение.

Теория вероятности — подходящий инструмент для ситуаций, когда мы просто не знаем весь набор причинно-следственных механизмов, определяющих исход ситуации, или для случаев, когда мы знаем, что влияет на исход, но наши теории трудно использовать на практике для получения надежных предсказаний. В таких случаях мы отказываемся от идеи предсказания конкретных исходов и вместо этого предсказываем, что, вероятно, случится, зная заранее возможные исходы. Вместо использования детерминистской модели, предсказывающей значение переменной x, например, предсказывая, что x=орел или x=решка, мы используем вероятностную модель, предсказывающую распределение случайной переменной X, например, предсказывая, что P(X=орлы)=1/2 и P(X=решки)=1/2, что эквивалентно указанию равномерного распределения X, то есть того, что все исходы имеют одинаковую вероятность.

Рассмотрим покупки всех жителей США за один месяц. Существует огромное количество причин, почему конкретные товары продаются в конкретных количествах по конкретным ценам. Некоторые товары покупают регулярно в одинаковых объемах, как, например, коммунальные услуги подачи газа или воды, другие товары мимолетны и их продажи зависят от быстро проходящей моды, например, на рынке детских игрушек. На продажи может влиять погода. Люди очень отличаются друг от друга, имеют различные цели и вкусы. Некоторые товары периодически изнашиваются и требуют замены. В общем, существует почти столько же причин для событий обмена, сколько и самих событий.

Разнообразие и непредсказуемость, неизбежно возникающие, когда сложные и разумные человеческие существа, конкурируя, взаимодействуют друг с другом, делают бесполезными попытки точного моделирования рыночного обмена. Хотя возможно смоделировать и предсказать поведение человека в контролируемых условиях эксперимента, ограничивающих пространство возможных действий, или в ситуациях, когда условности и правила играют важную роль, невозможно смоделировать ежедневное творчество участников рынка, стремящихся к удовлетворению своих целей в расширяющейся и взаимно создаваемой экономической среде. Очевидно, что если игнорировать особые случаи, то предсказание действительной цены товара в определенный день или предсказание спроса на вновь изобретенный товар, безнадежны. Цены и товары постоянно меняются. Рыночная экономика, следовательно, - идеальный кандидат для вероятностного моделирования.

6.1.1. Простая экономика обмена

Недавно физики занялись экономическими феноменами, создав новую дисциплину, называемую физической экономикой. Ее подходы к традиционным экономическим вопросам вероятностны по своей природе. Мы можем проиллюстрировать этот подход, рассмотрев очень простую модель рыночной экономики, разработанную физиками Драгулеску и Яковенко (Dragulescu, A. and Yakovenko, V. M.: 2000, Statistical mechanics of money, The European Physical Journal B 17, 723–729.).

Представьте простую экономику, состоящую из N человек, которых мы будем называть агентами. Каждый агент имеет деньги в количеств m, которые ради конкретности мы будем считать долларами. Общее количество денег в экономике, являющееся попросту суммой всех денег конкретных индивидов, - фиксированная константа M.

В рыночной экономике люди обменивают товары и услуги на какую-то сумму денег. Но мы полностью абстрагируемся от природы этих товаров и услуг, времени, в которое они производятся или продаются, от того, кто это делает и когда. Мы также не будем рассматривать институты, так что фирмы, банки и экономические операции государства выпадают из нашей картины. Вместо этого мы сосредоточимся на главных характеристиках динамической монетарной экономики — том факте, что деньги постоянно обмениваются между агентами в различном количестве, но почти всегда при этом сохраняются 1 . Мы не будем пытаться детерминистски смоделировать все отдельные причины, по которым конкретные агенты обмениваются определенными суммами денег в определенные моменты времени, а вместо этого предположим, что эту непредсказуемость можно смоделировать случайным шумом. При таком сильном абстрагировании динамику нашей простой модели можно выразить одним-единственным правилом:

Правило обмена Е₁:

1) Случайно выбрать агента i (1<=i<=N) при равномерном распределении. Агент i — покупатель.

2) Случайно выбрать агента j при равномерном распределении. Агент j — продавец.

3) Случайно выбрать цену p из интервала [0, m_i] при равномерном распределении, где m_i - количество денег у покупателя i.

4) Уменьшить количество денег у агента i на p. Увеличить количество денег у j на p.

Экономический обмен имитируется постоянным применением этого правила к экономике из N агентов. Правило перемещает случайные количества денег между случайно выбранными индивидами. Это всё. Считайте эту модель моделью простой экономики. Как уже указывалось, это очень простая модель. Она настолько проста, что сложно поверить, будто бы она способна углубить наше понимание экономики. Но на деле она воспроизводит одну из постоянных и характерных эмпирических регулярностей рыночной экономики.

Можно посчитать количество агентов с 0, 1, 2, ... М долларами в кармане. Каждую сумму можно считать группой, и любой конкретный агент в любый конкретный момент времени находится в одной из этих групп в зависимости от количества имеющихся у него денег. Например, если мы создадим модель так, что у каждого агента будет M/N долларов в кармане, а затем измерим размер каждой из групп, то обнаружим, что распределение денег вырождено. Все группы пусты, кроме M/N, которая имеет размер N. Распределение называется вырожденным, потому что имеется только одна возможность.

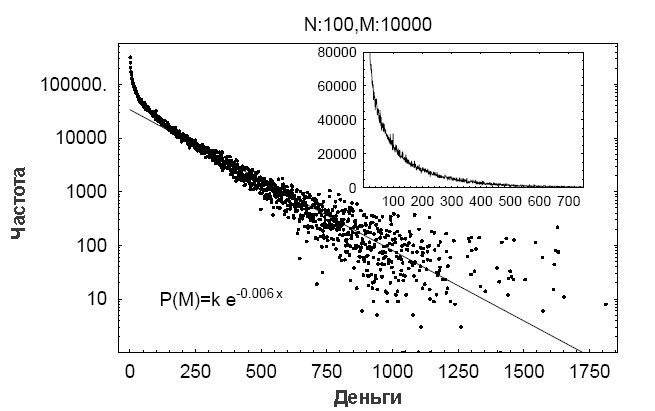
Но если применять правило E₁ много раз, допустим N² раз, распределение начнет отходить от вырожденного состояния по мере того, как деньги будут обмениваться в неравных количествах между агентами. Некоторым агентам повезет, они будут участвовать в удачных сделках и получат большое богатство, а другие будут все время терять деньги и мало что получать взамен. Если продолжать этот процесс, то экономика придет к распределению конкретного вида, показанному на рисунке 6.1.1. Такое распределение называется экспоненциальным. Врезка на рисунке показывает группы по оси х и количество агентов, входящих в эту группу, по оси y. Резко падающую кривую можно описать экспоненциальной функцией 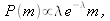что продемонстрировано прямой линией, соответствующей логарифмическому преобразованию данных. Распределение денег крайне неравномерно. У большинства агентов денег очень мало, а экспоненциально малое количество располагает большими суммами. Собственно, у очень малого количества людей имеется относительно огромное количество денег.

Рисунок 6.1.1. .Стационарное распределение богатства в простой экономике обмена, изображенное в логарифмической шкале. Прямая линия представляет распределение Больцмана, 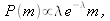Вставка - часть распределения богатства в стандартной шкале, которая более наглядно показывает, что у большинства агентов ценностей совсем немного, но экспоненциально немногие владеют большой частью богатства.

Интересно что экспоненциальное распределение богатства можно найти в настоящих данных настоящей экономики. Существует некоторое отклонение от экспоненциального распределения среди верхних 5-10% богатых, но в остальном оно правильно описывает огромную часть нашего населения (Nirei, M. and Souma, W.: 2003b, Income distribution and stochastic multiplicative process with reset events. http://www.santanfe.edu/makato/papers/income.pdf, Драгулеску (Dragulescu, A. A.: 2003, Applications of Physics to economics and finance: money, income, wealth and the stock market, PhD thesis, Department of Physics. http://arXiv.org/abs/cond-mat/0307341), Драгулеску и Яковенко (Dragulescu, A. and Yakovenko, V. M.: 2002, Statistical mechanics of money, income and wealth: a short survey. http://arXiv.org/abs/condmat/0211175)), какую бы развитую капиталистическую страну ни взять 2 . Распределение также стабильно в долговременном периоде. Хотя среднее количество богатства может меняться с каждым годом, общая форма его распределения остается экспоненциальной. Следовательно, простая вероятностная модель несмотря на сильную абстрактность и простоту (или благодаря им?) воспроизводит важное свойство современных капиталистических экономик.

Вероятностный подход также дает некоторые новые экономические идеи, в частности, важность статистического равновесия и энтропии в экономических феноменах.

6.1.2. Концепция статистического равновесия

Модель простой экономики иллюстрирует концепцию статистического равновесия. Со временем распределение богатства в экономике смещается к экспоненциальному и остается таким. Хотя экономические агенты продолжают обмениваться деньгами, увеличивать или уменьшать свой доход, общее распределение богатства в экономике остается постоянным.

Сравните такое равновесие с более известной концепцией механического равновесия. Например, рассмотрим весы: 1 кг на левой чашке и 1 кг на правой: весы находятся в равновесии, все силы равны, чашки весов неподвижны. Система находится в механическом равновесии и останется в нем, пока не будет приложена внешняя сила. Статистическое равновесие совсем другого типа. В отличии от механического, в котором конфигурация системы остается статической, система может находиться в статистическом равновесии, даже если ее конфигурация постоянно меняется. Распределение вероятности различных конфигураций системы — вот что не меняется с течением времени. Например, если изучим распределение денег в простой экономике в определенный период времени, а затем повторим исследование позже, оба распределения с большой вероятностью будут практически идентичны, несмотря на то, что деньги постоянно меняют хозяев. Следовательно, в отличие от механического равновесия, всегда существует вероятность, что система, находящаяся в статистическом равновесии, самопроизвольно из него выйдет. Но вероятность этого мала. Например, вероятность того, что простая экономика вдруг вернется к начальному равному распределению богатства так исчезающе мала, что ее можно считать невозможной.

Стандартные экономические теории, унаследованные нами от двадцатого века, являются детерминистскими моделями, следующими дорогой, проложенной теоретиками XIX века, копировавшими инструменты и методы господствующих в физических науках механических теорий (Mirowski, P.: 1989, More Heat Than Light: Economics as Social Physics, physics as Nature's Economics, Cambridge University Press.). Первую полную формулировку этого подхода можно найти в короткой книге Дебро «Теория стоимости» (Debreu, G.: 1959, Theory of value - an axiomatic analysis of economic equilibrium, Yale University Press, New Haven and London.), в которой рыночная экономика изображается как гигантский детерминистский калькулятор, вычисляющий из начального распределения товаров набор рыночных обменов между экономическими агентами, с которым согласны все. В этой модели концепция механического равновесия используется для понимания экономических феноменов. Но в отличие от механических конфигураций физических тел, которых иногда приходят в состояние покоя, рыночная экономика никогда не останавливается: это по своей природе динамическая система, с экономическими агентами, деятельность которых постоянно сбивает любую возможность достижения механического равновесия. Рыночная экономика больше похожа на мешок с камешками, который постоянно трясут, чем на пришедшие в равновесии весы.

Простейший случай статистического равновесия, изученный физическими науками, - это равновесие идеального газа. Идеальный газ состоит из миллионов одинаковых частиц, заключенных в совершенно непроницаемый контейнер. Каждая частица газа постоянно движется внутри контейнера, отскакивает от стен и других частиц, меняет направление, приобретает или теряет скорость в зависимости от случайностей, определяющих исход столкновения. На микроуровне это кажется хаосом. Но, несмотря на нескоординированный хаос, все частицы связаны друг с другом принципом сохранения энергии. При каждом столкновении сохраняется энергия, поэтому общая энергия системы постоянна. Следовательно, если одна частица движется очень быстро и имеет большую кинетическую энергию, отсюда с необходимостью следует, что некоторые другие частицы будут двигаться с меньшей скоростью. Физически невозможно, чтобы все частицы в один момент имели самую высокую кинетическую энергию. Другими словами, существует общий запас доступной энергии, который распределяется среди частиц газа. Эта общая энергия является на макроуровне ограничителем беспорядка микроуровня. Все возможные конфигурации системы, то есть возможные распределения кинетической энергии среди частиц газа, не могут нарушать это глобальное ограничение.

Фундаментальный закон равновесия в статистической механике — это закон Больцмана-Гиббса, который дает распределение вероятности энергии 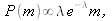где 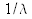- температура газа или средняя энергия, приходящаяся на одну частицу. Мы опять сталкиваемся с экспоненциальным распределением. Это неудивительно, если заметить, что модель простой экономики и идеальный газ формально эквивалентны.

6.1.3. Распределение с максимальной энтропией

В разделе 1.4. рассказывалось о втором законе термодинамике. Этот закон постулирует, что полная энтропия в закрытой системе только возрастает. Простая экономика и идеальный газ — это закрытые системы. Из второго закона вытекает, что равновесное распределение, которое, как мы наблюдали, оказалось экспоненциальным, должно быть распределением, в котором энтропия максимальна, при учете общего ограничения на количество денег в экономике (или общей энергии газа). Давайте проверим. Рассмотрим следующую меру энтропии для простой экономики:

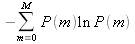(6.1)

где P(m) — вероятность того, что случайный выбранный агент располагает деньгами в количестве m. В экономике M агентов и N долларов, и то, и другое сохраняется. Пусть n_m — количество агентов, располагающих m долларами. Обязательно выполняются такие условия:

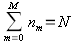
и

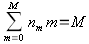
Вероятность того, что случайно выбранный агент будет располагать деньгами m равна P(m)=n_m/N. Если мы подставим n_m=P(m)N в приведенные выше два уравнения, то получим два ограничения на вероятности:

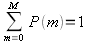
- простое ограничение, что сумма всех вероятностей должна быть равна единице и

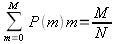
- ограничение, что вероятности должны соответствовать ограничению на общее богатство.

Математическая задача - найти формулу для P(m), учитывающую ограничения и максимизирующую значение энтропии. Задача может быть решена многими способами, подробности которых для нас не важны 3 . Оказывается, что решение на самом деле — (экспоненциальное) распределение Больцмана-Гиббса 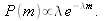Экспоненциальное распределение богатства, следовательно, - наиболее беспорядочное распределение, которого можно достичь при единственном ограничении на систему — сохранении энергии. Ясно, что если экономическая система состоит из более сложных агентов типа «экономических демонов», которые, например, создали союзы или разработали совместные планы, направленные на сознательное изменение распределения доходов, тогда необходимо вводить новые ограничения на вероятности, и математические рассуждения будут другими. Но тот факт, что большинство полученных эмпирическим путем распределений доходов в капиталистических экономиках оказываются экспоненциальными, говорит о том, что такие факторы не являются значимыми.

В реальности, в отличие от модели простой экономики, существует множество схем перераспределения денег, например, ограниченное перераспределение дохода через государственные налоги. Удивительно, но подобные механизмы не влияют на общую функциональную форму распределения доходов. Рынки имеют очень прочную тенденцию к максимизации энтропии. Они создают крайне неравномерные, преимущественно экспоненциальные, распределения доходов.

Мы вернемся к вопросу распределения доходов в главе 9, где узнаем, что полное распределение доходов имеет меньшую энтропию, чем экспоненциальное. Поэтому действуют еще какие-то причины, отсутствующие в модели простой экономики, налагающие дополнительные ограничения на вероятности P(m). Отсюда следует, что проводится какая-то уменьшающая энтропию работа «демонов», результатом которой становится «сортировка» денег между различными экономическими классами.

6.1.4. Случайные агенты и рациональные агенты

В этом месте можно возразить, что экономические агенты явно целенаправленны, и поэтому необходимо моделировать индивидуальную рациональность даже при исследовании на макроуровне, например, исследуюя возникающее распределение доходов. Например, люди не обмениваются деньгами по случайным правилам и, в зависимости от участвующих сумм, часто очень тщательно размышляют над своими тратами. Но это возражение смешивает эпистемологию с онтологией, картинку с реальностью. Из случайной модель совсем не обязательно вытекает, что причинно-следственные связи, которые она представляет, случайны, а только лишь, что очень трудно смоделировать все причинно-следственные связи с большой точностью. Случайность здесь представляет все множество различных рациональных (или не очень) решений экономических агентов.

Экономическая теория рационального агента предполагает, что феномены макроуровня сводимы к механизмам индивидуальной рациональности и объясняются ими. Фарджун и Маховер (Farjoun, E. and Machover, M.: 1983, Laws of Chaos, a Probabilistic Approach to Political Economy, Verso, London.) заметили, что успешно работающая физическая теория статистической механики прямо противоречит этому предположению. Например, классическая статистическая механика моделирует молекулы газа в виде идеализированных совершенно упругих бильярдных шаров. Конечно же, это огромное упрощение структуры молекулы и ее взаимодействия с другими молекулами. Однако статистическая механика может вывести факты макро-уровня, проходящие проверку опытом. Цитируя Хинчина (Khinchin, A. I.: 1949, Mathematical foundations of statistical mechanics, Dover Publications):

Эти общие законы механики, используемые в статистической механике, необходимы для любого движения материальных частиц вне зависимости от сил, вызывающих такое движение. Именно полное абстрагирование от природы этих сил придает статистической механике ее особенные свойства и дает ее выводам необходимую гибкость... особенный характер систем, изучаемых статистической механикой, состоит главным образом в огромном числе степеней свободы, которыми располагает эта система. Методологически это означает, что точка зрения статистической механики определяется не ее механической природой, а молекулярной структурой материи. Может даже показаться, что цель статистической механики — понять, насколько далеко идущие выводы можно сделать на основе атомного строения материи, вне зависимости от природы этих атомов и законов их взаимодействия.

Метод абстрагирования от механики индивидуальной рациональности и введения структуры индивидов-частиц имеет смысл, потому что число степеней свободы экономической реальности очень велико. Мы можем описать индивидуальное решение как крайне упрощенный случайный выбор из возможностей, ограниченных общими принципами макроуровня, такими как сохранение денег. На этом уровне абстракции индивидуальную психологию можно смоделировать как дополнительный шум.

Глава 8. Теория цен Фарджуна и Маховера

Когда Шайк и другие эмпирические исследователи начали в 1984 году публиковать свои результаты, последние стали сюрпризом для экономистов, которые обратили на них внимание. Но годом раньше появилась знаменательная книга «Законы хаоса» (Фарджун и Маховер, 1983). В книге, написанной двумя физиками, доказывалось, что экономисты ошибаются, пытаясь сконструировать полностью детерминистские теории. Авторы указывали, что еще начиная с Больцмана, физики могли делать полезные предсказания об общем поведении систем, которые в малом масштабе кажутся случайными и хаотическими.

В малом масштабе движение молекул газа или жидкости случайно, и это случайное движение можно даже, как указал в 1905 году Эйнштейн, увидеть в форме броуновского движения — наблюдаемых под микроскопом колебаний маленьких частичек, например, пыльцы, в воде. Но в большом масштабе эти случайные движения усредняются, что позволяет делать полезные обобщения: законы газа, законы термодинамики. Фарджун и Маховер утверждали, что экономисты застряли в модели причинности образца начала XIX века. Если ее оставить, то становятся возможными несколько различных способов рассуждений об экономике. Практически полностью обойдясь без ортодоксальных экономических теорий, авторы вывели несколько интересных обобщений о работе капиталистических экономик. Одним из них было предсказание тесной корреляции рыночных цен с трудовыми стоимостями.

В науке предсказания всегда более убедительны, чем «послесказания». Тот факт, что теоретические результаты Фарджуна и Маховера были вскоре подтверждены эмпирическими исследованиями, придало им вес, особенно, если учесть, что предсказания совершенно противоречили общепринятым в экономике мнениям Мы вряд ли сможем полностью изложить их теорию в нашей работе. Поэтому мы расскажем о ней упрощенно, опустив почти всю математическую строгость, но достаточно для интуитивного понимания механизма, который они предложили в качестве объяснения закона стоимости.

Рассмотрим все товары, проданные фирмами одной страны в течение недели. Это будет длинный список товаров и услуг, дорогих и дешевых. Некоторые требуют для своего производства большое количество труда, некоторые — нет. Предположим, что закон стоимости действует и цены товаров примерно пропорциональны содержанию в них труда. Как мы можем это измерить?

Фарджун и Маховер ввели случайную переменную Ψ, которая означает среднюю цену труда в течение часа. Идея состоит в том, что мы выражаем все производство различных товаров: аэробусов А380, шоколадных бисквитов, одноразовых носовых платков и т.д. в терминах содержания в них труда. Затем мы делим его на единицы по часу каждая и представляем, что случайно выбираем часы из этого огромного списка. Затем мы смотрим, чему соответствуют эти часы, выраженные в деньгах.

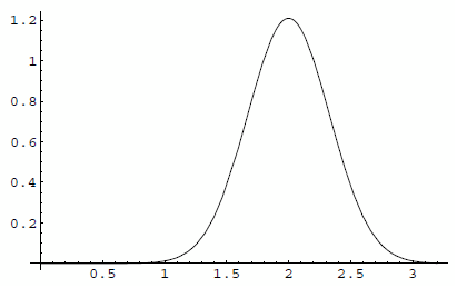
Ученые предсказали, что если изобразить частоту различных значений Ψ, наблюдаемую на достаточно большой выборке товаров, тогда распределение будет выглядеть так, как на рис. 8.1. Оно должно принять форму колоколообразной кривой, соответствующей тому, что статистики называют нормальным распределением.

Рис. 8.1. Предсказанная Фарджуном и Маховером форма связи Ψ между трудовой стоимостью и ценой

Нормальное распределение, как указывает само его название – это одно из наиболее часто встречающихся видов распределения. Многие наблюдения воплощаются в такой форме. Например, если нарисовать на графике высоту десятилетних мальчиков из Лондона, то получится нормальное распределение. Если нарисовать тщательно измеренный вес достаточно большого количества одинаковых монет, получится нормальное распределение. Если нарисовать количество фотонов, приходящих за секунду в телескоп с какой-нибудь удаленной звезды, получится нормальное распределение. Собственно, всегда, когда величина, которую измеряют, является результатом сложения большого количества случайных независимо действующих причин, распределение, которое получится на графике, будет знакомой колоколообразной кривой нормального распределения.

Нормальное распределение N(μ,σ) характеризуется двумя числами: математическим ожиданием (μ), характеризующим вершину распределения, и стандартным отклонением (σ), описывающим ширину колокола кривой. Фарджун и Маховер предсказали, что график зависимости цен от трудовых стоимостей будет иметь матожидание 2 и стандартное отклонение, меньшее 1/3. Как они пришли к такому выводу?

Во-первых, почему они утверждают, что матожидание равно двум, то есть средняя цена товара будет в два раза выше его трудовой стоимости?

Частично это зависит от выбранной ими единицы измерения. Как только вы попытаетесь создать теорию цен, перед вами станет вопрос единицы расчетов. Когда мы хотим измерить расстояние, мы можем воспользоваться метрами, которые, в свою очередь, определены в терминах естественных констант – длины волны определенного света. С их помощью получается стандарт, не зависящий от пространства и времени. Но чем мы можем измерить цены?

Если мы используем деньги, то должны это быть доллары, евро или йены?

Если мы будем применять одну из валют, как мы сможем учесть инфляцию?

Чтобы решить эту проблему, Фарджун и Маховер используют технику, одобренную Адамом Смитом и Мейнардом Кейнсом. Они используют как единицу измерения среднюю часовую зарплату. Смит, как мы видели, считал, что настоящей ценой любого товара является количество труда, которое он получает в свое распоряжение. Фарджун и Маховер были чуть-чуть точней и определили действительную цену товара, для производства которого требуется час труда, как количество часов труда, оплачиваемых по средней часовой ставке, которыми он может распоряжаться. Предположим, что четыре килограмма трески для доведения до товарной кондиции требуют часа прямого и косвенного труда. Предположим также, что эту треску можно продать за 15 фунтов, а средняя часовая ставка равна 6 фунтам. В терминологии Фарджуна и Маховера:

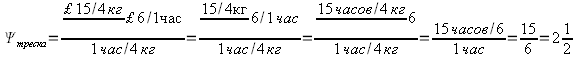
Мы можем ожидать, что Ψ будет >1, поскольку продажную цену товара можно, как показал Смит, разложить на зарплату и прибыль 4 . Продажная цена уходит на выплату зарплаты, прибыль и издержки на сырье. Но стоимость сырья можно точно также разложить на зарплаты, прибыль и стоимость сырья. Если вы будете двигаться все дальше и дальше, то обнаружите, что конечная доля сырья стремится к нулю, поэтому можно сказать, что вся продажная цена в конце концов делится на зарплату и прибыль 5 .. Поскольку Фарджун и Маховер сочли, что в большинстве капиталистических стран добавленная стоимость распределяется между зарплатой и прибылью поровну, отсюда следует, что средняя цена продукта в рабочих часах будет в два раза выше средней стоимости часа труда.

Это объясняет, почему они считают, что матожидание 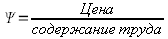равно 2. Почему они определяют стандартное отклонение равным 1/3 ?

Доказательство очень простое. Они указывают, что товары очень редко продаются так дешево, что продажной цены будет недостаточно для уплаты прямой и косвенной зарплаты, необходимой для их производства. Граница проходит при значении Ψ = 1. Кроме этого, производство товара будет невыгодным, если оно не покрывает расходов даже на прямую зарплату. Они предполагают, что существует только один шанс из тысячи, что товар будет продаваться дешевле стоимости своего производства.

Посмотрев в таблицу нормального распределения, можно узнать, что вероятность того, что отклонение от средней составит 3 стандартных отклонения, равна около 1/1000, отсюда они выводят, что 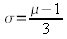, поэтому для μ равного двум, ? должно быть равно 1/3.

Как эти предсказания соотносятся с реальными данными? Используя данные по Англии за 1984 год – год после выхода книги Фарджуна и Маховера – мы рассчитали 6 , что Ψ хорошо ложится в распределение с μ=1,46 и σ = 0,151.

На первый взгляд, результаты сильно отличаются от предсказанных. Но разница почти целиком объясняется тем фактом, что в 1984 году в Великобритании добавленная стоимость распределялась между прибылью и зарплатами в соотношении один к двум вместо равного, предполагаемого Фарджуном и Маховером. 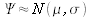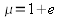Полная форма их предсказания имеет следующий вид: если e есть отношение агрегатной прибыли к агрегатной зарплате, то при и 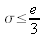. Если мы подставим правильное значение e в данные для Великобритании 1984 года, то получим почти точное соответствие.

Из этой теории вытекает интересное следствие: связь между ценами и трудовыми стоимостями будет сильнее, когда доля прибыли в национальном доходе меньше. Если доля прибыли в национальном доходе уменьшается, тогда можно ожидать, что относительные рыночные цены будут больше приближаться к относительным трудовым стоимостям. Из-за прибыли отношение сигнала к шуму для цен увеличивается.

Распределение Ψ случайно или энтропийно. Можно рассчитать энтропию нормально распределенной случайной переменной, применяя модифицированную формулу Шеннона. Шеннон определял энтропию сигнала как

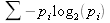
где i принимает набор дискретных величин, соответствующих различным различимым состояниям сигнала. Нормальное распределение N(?,?) – это плотность вероятности. Это функция, определенная на поле действительных чисел, такая что

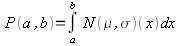
определяет вероятность того, что x будет находиться в интервале a..b. Если мы подставим ее в формулу Шеннона и численно проинтегрируем, то сможем рассчитать энтропию нормального распределения при заданном стандартном отклонении.

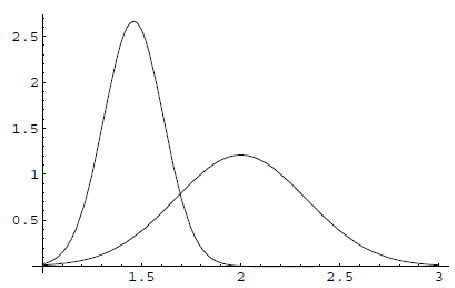
Мы обнаружили таким образом, что нормальные распределения с малым стандартным отклонением обладают низкой энтропией, а с большим отклонением – высокой энтропией. На рисунке 8.2 показано распределение Ψ, предсказанное Фарджуном и Маховером, а рядом для сравнения нормальное распределение с математическим ожиданием и стандартным отклонением, наблюдавшимся в Великобритании в 1984 году. Энтропия более широкой кривой справа около 7,1 битов, той, что слева, - около 5,9 битов.

Рис. 8.2. Предсказанная Фарджуном и Маховером Ψ(справа) и Ψ по результатам измерений в Великобритании в 1984 году (слева).

Примечания

1  В 1994 году шотландские художники-авангардисты Билл Драммонд и Джимми Каути сожгли миллион фунтов стерлингов, заработанны[ на продаже поп-записей. Но такие события имеют малую вероятность.

2  Некоторые эмпирические исследования использовали доход за определенный период времени как показатель имеющегося на данный момент богатства, но такие тонкости здесь не важны.

3  Заинтересовавшемуся читателю стоит посмотреть Капур (Kapur, J. N.: 1989, Maximum Entropy Models in Science and Engineering, Wiley Eastern Limited.) и Капур и Кесаван (Kapur, J. N. and Kesavan, H. K.: 1992, Entropy optimization principles with applications, Academic Press Inc.).

4  Смит также выделял часть для уплаты ренты, но Фарджун и Маховер игнорируют ее, потому что сейчас рента актуальна гораздо меньше, чем в XVII столетии.

5  Маркс возражал, считая, что стоимость сырья никогда нуля не достигнет. В качестве математического возражения это звучит не слишком серьезно, поскольку стоимость сырья экспоненциально стремится к нулю. Как социологическое возражение это имеет определенный смысл, поскольку капиталистическое производство предполагает существование капиталистов, владеющих сырьем, средствами производства и нанимающих труд. Если бы сырье и средства производства не находились в руках капитала, тогда рабочие забирали бы себе весь доход и не было бы деления на зарплату и прибыль. С учетом этой социологической тонкости математическое приближение Смита выглядит разумным.

6  Результат взят из книги (Cockshott, W. P. and Cottrell, A. F.: 1998, Does marx need to transform?,in R. Bellofiore (ed.), Marxian Economics: A Reappraisal, Vol. 2, Basingstoke, pp. 70–85) с небольшим изменением определения Ψ в соответствии с используемым Фарджуном и Маховером.